Solving a Thermal-Mechanical Problem in Hydroforming L-Foot Fins for Heat Exchanger Tubes Using Finite Element Analysis

Heat exchangers and condensers are an essential component in many industries, such as chemical, power generation, and refrigeration. They transfer heat between two fluids, which can be gases or liquids, without them coming into contact with each other. Heat exchangers are designed to maximize heat transfer efficiency while minimizing the size, weight, and cost of […]
Cálculos estructurales para la moto eléctrica VMS Eezon 3

SDEA_Engineering Solutions ha realizado los cálculos estructurales para la moto eléctrica VMS Eezon 3. Este vehículo de tres ruedas, pensado para flotas y servicios, es un concepto novedoso pensado para mejorar la operatividad del reparto en ciudad, con una elevada capacidad de carga y una drástica reducción de emisiones respecto a los métodos de transporte […]
Bellows Expansion Joint Analysis using FEA
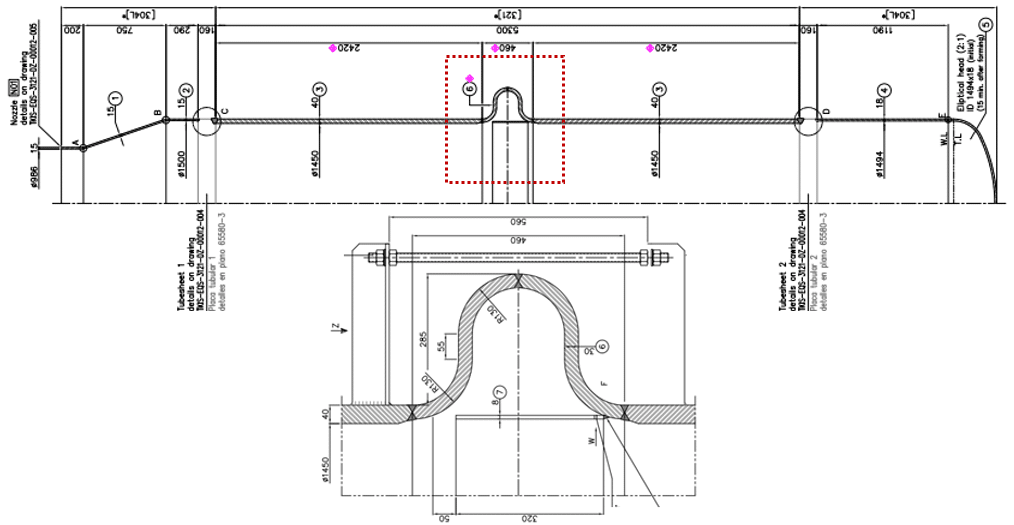
This example is a heat exchanger with a bellow expansion joint and the reason of performing this study is because of a transition zone between two parts with different thickness, in order to assess the failure risk in that zone.
Pressure Vessels Design
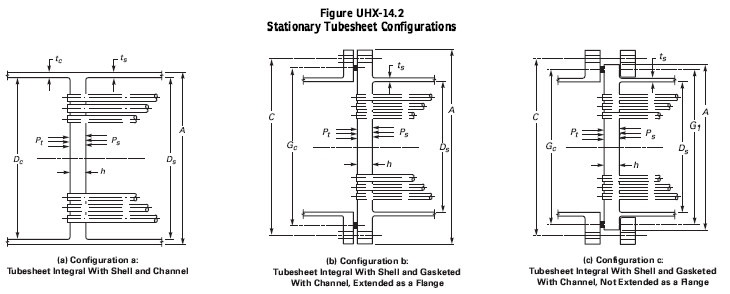
Pressure Vessels are used in the industry to store process fluids under certain temperature and pressure conditions. Commonly, pressure vessels have cylindrical or spherical shape, can be disposed in a horizontal or vertical way and are provided of heads with different shapes (Ellipsoidal, Hemispherical, Toroidal, etc.). These equipments are fitted with different elements such as nozzles (used […]
Thermal Stress Analysis Of Dissimilar Welding Joints using FEA

Finite Element to foreseen residual stress from the welding process Most welding process involve local heating, therefore temperature distribution is not uniform and structural thermal stresses beyond the material yield [strongly dependent on the temperature] show up, which can create issues on the final design related to fatigue or even geometry distortions. This local temperature […]
TLD Tuned Liquid Dampers

FEA for TLD Tuned Liquid Dampers One of the greatest challenges when it comes to design steel stack structures such as chimneys, is to deal with oscillating loads as dynamic wind forces and seismic spectrum, as commented in this article. These loads threaten the design with coupling the excitation with its natural frequency, leading the […]
FSI Steel Stack Structural FEA Analysis
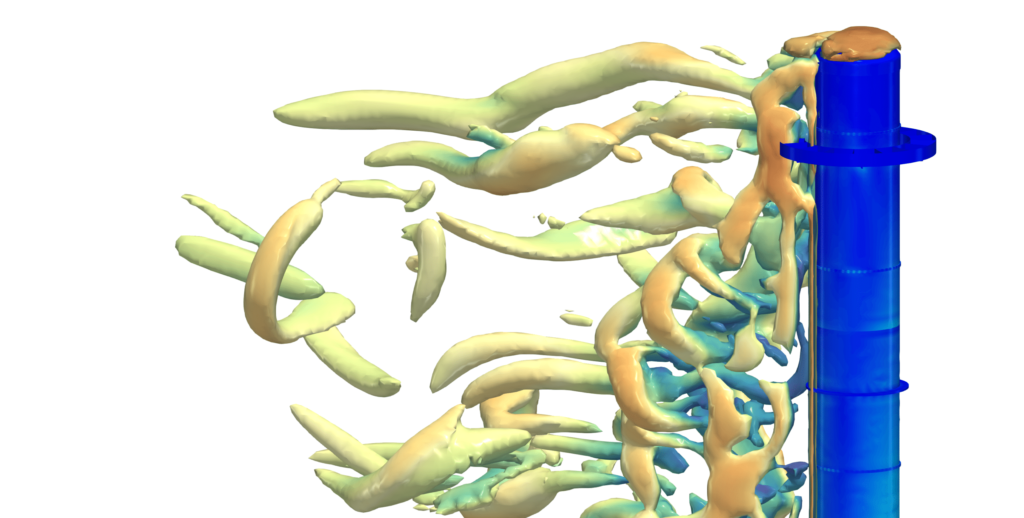
Chimney miniature When designing steel stack structures, several rules from standards as “ASME STS-1” or “ASCE 7” have to be taken into consideration to assure security during its useful life. This is particularly important for those located in areas subjected to heavy environmental loads, such as high activity seismic zone 4, due to the slender […]

